Basic example cytometry workflow¶
Welcome to cytoflow! I’m glad you’re here. The following is a
heavily commented workflow for importing a few tubes of cytometry data
and doing some (very) basic analysis. The goal is to give you not only a
taste of using the library for interactive work, but also some insight
into the rationale for the way it’s designed the way it is and the way
it differs from existing projects.
cytoflow’s goal is to enable quantitative, reproducible cytometry
analysis. Reproducibility between cytometry experiments is poor, due in
part to differences in analysis between operators; but if all your
analysis is in a Jupyter notebook (like this one!), then sharing and
reuse of workflows is much easier.
Let’s look at a very basic experiment, containing only two tubes. These two tubes contain cells that are expressing fluorescent proteins as the read-out of some cell state. We’ll assume that these two tubes are identical, except that one has been induced with 1 µM of the small molecule inducer Doxycycline (aka ‘Dox’) and the other tube has been induced with 10 µM Dox.
Start by setting up Jupyter’s plotting interface, then import the
cytoflow module.
# in some buggy versions of the Jupyter notebook, this needs to be in its OWN CELL.
%matplotlib inline
import cytoflow as flow
# if your figures are too big or too small, you can scale them by changing matplotlib's DPI
import matplotlib
matplotlib.rc('figure', dpi = 160)
The central data structure in cytoflow is the Experiment, which
is basically a pandas.DataFrame containing the events; its
associated metadata (experimental conditions and the like); and some
methods to manipulate them.
You usually create an Experiment using an instance of the
ImportOp class. Start by defining two tubes, including their
experimental conditions (ie, how much Dox is in each); then give those
tubes, and a dict specifying the experimental conditions’ names and
types, to ImportOp. Call the apply() function to get back the
Experiment with all the data in it.
tube1 = flow.Tube(file = 'data/RFP_Well_A3.fcs',
conditions = {'Dox' : 10.0})
tube2 = flow.Tube(file='data/CFP_Well_A4.fcs',
conditions = {'Dox' : 1.0})
import_op = flow.ImportOp(conditions = {'Dox' : 'float'},
tubes = [tube1, tube2])
ex = import_op.apply()
Once you have an Experiment instance, this is the last time you
should ever think about tubes or wells. Rather, think of your experiment
as a very large set of single-cell measurements, each of which has some
metadata associated with it; in this case, how much Dox the cell was
exposed to. cytoflow helps you focus your analysis on how those
measurements change as the experimental conditions change, without
worrying about what cells were in what tube.
Let’s have a quick look at one of the fluorescence channels, Y2-A.
Instantiate a HistogramView and tell it which channel we’re looking
at, then call plot and pass it the experiment containing the data.
Remember, this is not a single tube, but rather all the data in the
Experiment.
hist = flow.HistogramView()
hist.channel = 'Y2-A'
hist.plot(ex)
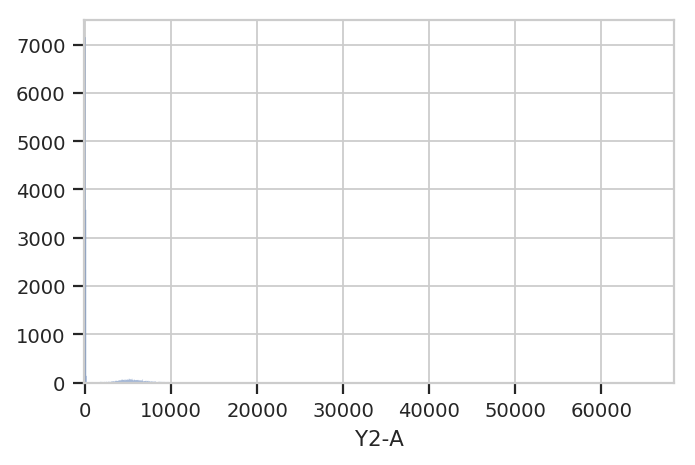
Hmmm. This plot is hard to interpret because most of the data is
clustered around 0, in the linear range of the detector’s response.
Let’s re-plot using a different scale. My favorite is logicle, which
has a linear response around 0 and a log range elsewhere. We specify the
plot scale by setting the scale attribute of HistogramView to
logicle; other options are log and linear.
The cell below also demonstrates a different way to parameterize the
HistogramView instance, by passing parameters to the constructor
instead of setting the values of the instance’s attributes after we make
it. Either way is correct.
hist = flow.HistogramView(channel = 'Y2-A',
scale = 'logicle')
hist.plot(ex)
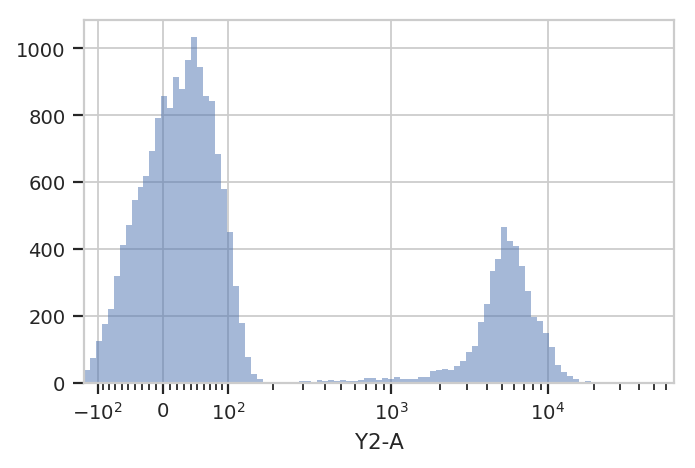
Ah, much better. There is clearly a population of cells around 0 and a
population of cells around about 5000. But! This is the entire
Experiment – is is one of the populations from the low-Dox tube and
the other population from the high-Dox tube?
Let’s see if the histogram is different for the two different
concentrations of inducer. CytoFlow’s plotting takes inspiration
from Trellis plots (eg the lattice package in R): to split the data into
subsets, you tell the plotting module which metadata “facet” you want to
plot in the X, Y and color (hue) axes.
This time, we tell HistogramView to make a separate plot for each
different value of Dox and stack them on top of eachother by saying
yfacet = 'Dox'; if we wanted the plots side-by-side, we would have
said xfacet = 'Dox'.
Also note that this time, we don’t keep around the HistogramView
object; if we don’t need to re-use it, we can just call plot right
after the constructor.
flow.HistogramView(channel = 'Y2-A',
scale = 'logicle',
yfacet = 'Dox').plot(ex)
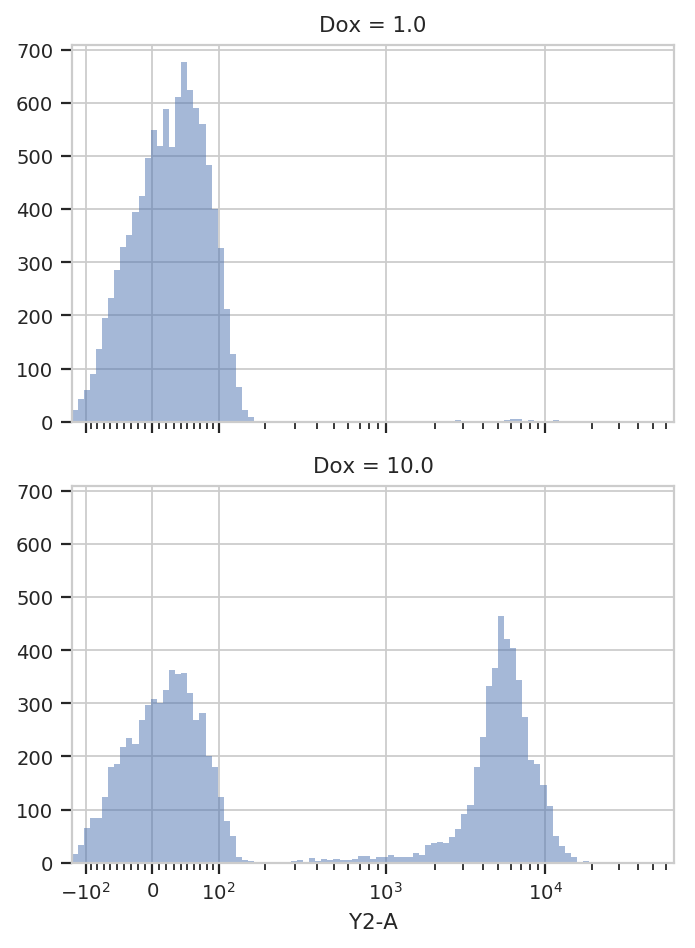
Indeed, the two tubes have dramatically different histograms. We could
also plot them on top of eachother with different colors, by using
huefacet instead of yfacet.
flow.HistogramView(channel = "Y2-A",
scale = "logicle",
huefacet = 'Dox').plot(ex)
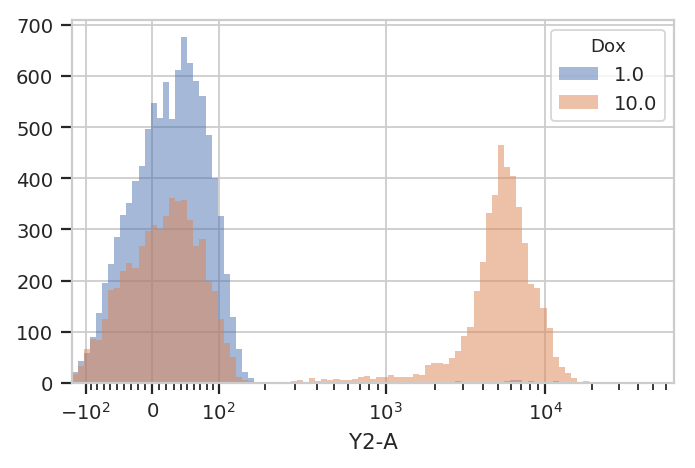
So, there’s a clear difference between these tubes: one has a
substantial population above about ~200 in the Y2-A, and the other
doesn’t. What’s the proportion of “high” cells? Let’s gate out the
“high” population using a ThresholdOp.
thresh = flow.ThresholdOp(name = "T",
channel = "Y2-A",
threshold = 200)
ex2 = thresh.apply(ex)
Two important things to note here: first, an Operation (such as
ThresholdOp) does not operate in place; instead, you create a
ThresholdOp object, then call apply() to run it on an
Experiment. The apply() function returns a new Experiment.
Second, a gate does not remove events; it simply adds additional
metadata to the events already there. You can see this if we look at
the underlying pandas.DataFrame for ex and ex2:
print(ex.data.head())
print("----")
print(ex2.data.head())
B1-A B1-H B1-W Dox FSC-A FSC-H 0 -127.094002 257.718353 -63040.300781 10.0 459.962982 437.354553
1 -70.234840 255.798340 -34034.042969 10.0 -267.174652 365.354553
2 -96.471756 313.398346 -41931.687500 10.0 -201.582336 501.354553
3 18.831570 277.669250 8514.489258 10.0 291.259888 447.029755
4 100.882095 255.756256 51291.074219 10.0 -397.168579 354.565308
FSC-W HDR-T SSC-A SSC-H SSC-W 0 137847.578125 2.018511 840.091370 747.917847 147225.328125
1 -95849.679688 27.451754 3476.902344 3163.917969 144038.046875
2 -52700.828125 32.043865 480.270691 507.917877 123937.437500
3 85399.273438 79.327492 8026.275879 6741.838867 156043.484375
4 -146821.125000 79.731194 7453.750488 609.884277 262143.968750
V2-A V2-H V2-W Y2-A Y2-H 0 41.593452 240.153854 22701.017578 109.946274 153.630051
1 103.437637 336.153870 40332.058594 5554.108398 4273.629883
2 -271.375580 256.153870 -138860.828125 81.835281 121.630051
3 -26.212378 207.677841 -16543.453125 -54.120304 98.122017
4 44.559933 216.036865 27035.013672 -10.542595 127.326027
Y2-W
0 93802.468750
1 170344.203125
2 88188.023438
3 -72294.242188
4 -10852.761719
----
B1-A B1-H B1-W Dox FSC-A FSC-H 0 -127.094002 257.718353 -63040.300781 10.0 459.962982 437.354553
1 -70.234840 255.798340 -34034.042969 10.0 -267.174652 365.354553
2 -96.471756 313.398346 -41931.687500 10.0 -201.582336 501.354553
3 18.831570 277.669250 8514.489258 10.0 291.259888 447.029755
4 100.882095 255.756256 51291.074219 10.0 -397.168579 354.565308
FSC-W HDR-T SSC-A SSC-H SSC-W 0 137847.578125 2.018511 840.091370 747.917847 147225.328125
1 -95849.679688 27.451754 3476.902344 3163.917969 144038.046875
2 -52700.828125 32.043865 480.270691 507.917877 123937.437500
3 85399.273438 79.327492 8026.275879 6741.838867 156043.484375
4 -146821.125000 79.731194 7453.750488 609.884277 262143.968750
V2-A V2-H V2-W Y2-A Y2-H 0 41.593452 240.153854 22701.017578 109.946274 153.630051
1 103.437637 336.153870 40332.058594 5554.108398 4273.629883
2 -271.375580 256.153870 -138860.828125 81.835281 121.630051
3 -26.212378 207.677841 -16543.453125 -54.120304 98.122017
4 44.559933 216.036865 27035.013672 -10.542595 127.326027
Y2-W T
0 93802.468750 False
1 170344.203125 True
2 88188.023438 False
3 -72294.242188 False
4 -10852.761719 False
In ex2, the ThresholdOp added a new column, named T, which has
the same name as the ThresholdOp’s name attribute. It is
True if the Y2-A value is greater than 200, and False
otherwise. The T column is now a piece metadata just like the Dox
concentration that we can use to facet the plots. For example, the
following plots different Dox concentrations in separate plots
stacked on top of eachother (yfacet = "Dox"), and on each of these
plots uses separate colors for the “low” and “high” populations
(huefacet = 'T'):
flow.HistogramView(channel = "Y2-A",
scale = "logicle",
yfacet = "Dox",
huefacet = 'T').plot(ex2)
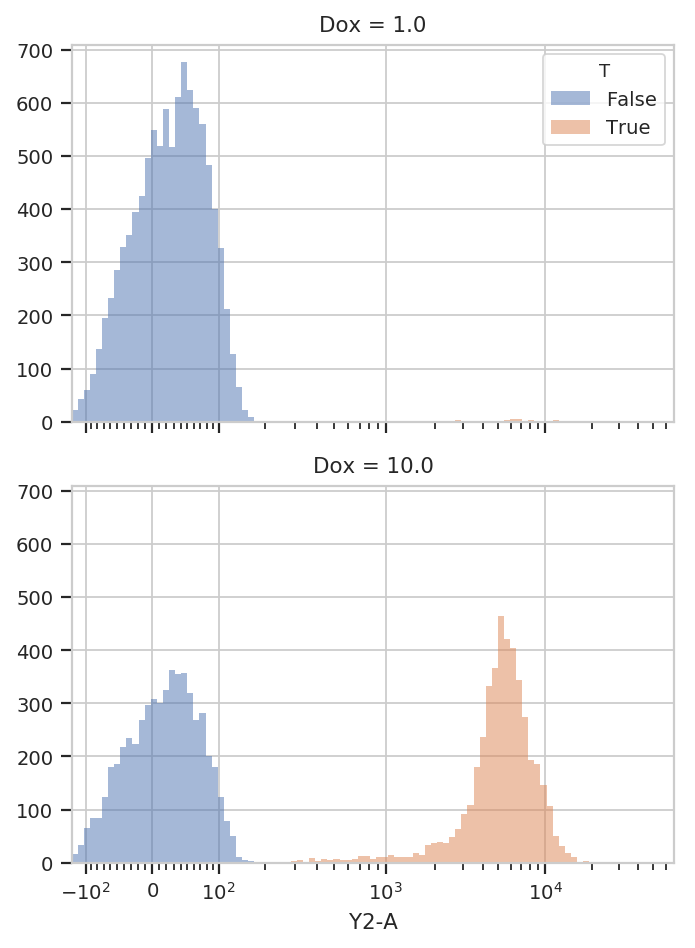
It’s also important to note that we can still access the underlying
pandas.Dataframe: either by looking at the Experiment.data
attribute, or by referencing a column directly:
ex2["T"].head(10)
0 False
1 True
2 False
3 False
4 False
5 False
6 True
7 False
8 True
9 False
Name: T, dtype: bool
Because the data is all stored in a single pandas.Dataframe, we can
use the pandas API, and indeed the rest of the SciPy stack, to ask
sophisticated questions of the underlying data. For example, “how many
events of each Dox concentration were above the threshold?”
ex2.data.groupby(['Dox', 'T']).size()
Dox T
1.0 False 9946
True 54
10.0 False 5561
True 4439
dtype: int64
cytoflow can answer the same question for us using one of its
statistics views. In cytoflow, a statistic is a number that
summarizes a population; one of the key features of cytoflow is that
it makes it easy to see how these summary statistics change as your
experimental conditions change.
Several operations add statistics to an experiment; one of the most
straightforward ones is ChannelStatisticOp. It groups the
experiment’s data by the conditions specified in by, then applies
function to channel for each group.
In this case, we’ll divide up the data into the subgroups
T == True & Dox == 1; T == True & Dox == 10;
T == False & Dox == 1; and T == False & Dox == 10. Then, we’ll
apply the function len to the Y2-A channel.
ex3 = flow.ChannelStatisticOp(name = "ByDox",
channel = "Y2-A",
by = ['T', 'Dox'],
function = len).apply(ex2)
Now we can look at the new statistic: Experiment.statistics is a
dictionary whose keys are tuples and whose values are the computed
statistics (stored as MultiIndexed pandas.Series). The first
element in the tuple is the name of the operation that added it, and the
second is defined by that operation. In this case, it’s len, the
name of the function.
ex3.statistics[("ByDox", "len")]
T Dox
False 1.0 9946
10.0 5561
True 1.0 54
10.0 4439
Name: ByDox : len, dtype: int64
We can also plot statistics using one of the various statistics views,
such as BarChartView.
flow.BarChartView(statistic = ("ByDox", "len"),
variable = "Dox",
huefacet = 'T').plot(ex3)
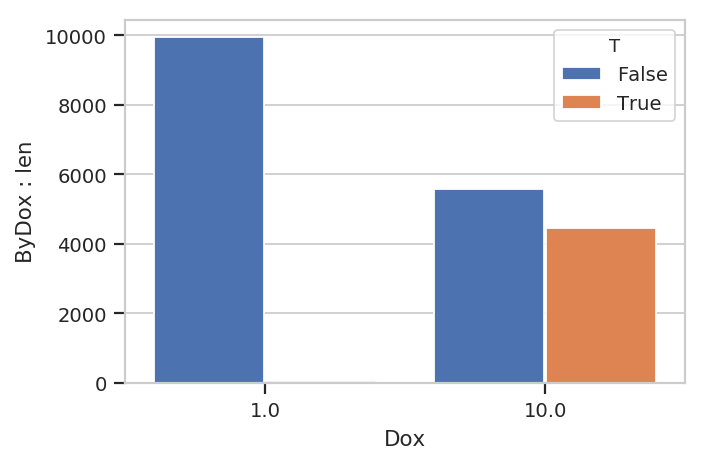
Statistics are important enough that they get an entire notebook of
examples; please see Statistics.ipynb for a more in-depth
exploration.
I hope this makes the semantics of the cytoflow package clear. This
was a pretty simplistic toy analysis; for more sophisticated examples,
see the other accompanying Jupyter notebooks.